ÁLGEBRA Y FUNCIONES

 1. POLINOMIOS

SUMA Y RESTA DE POLINOMIOS

Recuerda que basta con sumar o restar los monomios que sean semejantes, es decir, que tengan la misma parte literal.

RECUERDA: Monomio: es el producto de un número conocido (coeficiente) por uno o varios valores desconocidos, representados por letras (parte literal). El grado de un monomio es el número de factores que forman su parte literal (la suma de los exponentes de las letras).

PRODUCTO DE POLINOMIOS

Hay que multiplicar cada monomio del primer polinomio por todos los términos del segundo monomio y luego agrupar todos los términos semejantes.

Multiplicación de un polinomio por un número

El producto de un escalar (o un número) por un polinomio es bastante fácil de resolver, simplemente se debe multiplicar el número por el coeficiente de cada término del polinomio.

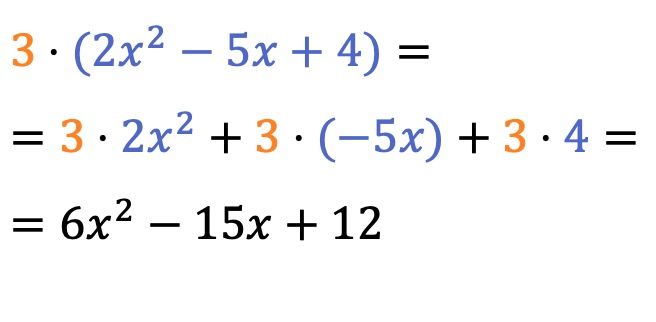
El signo de multiplicación de delante del paréntesis se puede omitir.

Multiplicación de un polinomio por un monomio

Antes de ver cómo multiplicar un polinomio por un monomio, primero vamos a recordar cómo se multiplican los monomios entre sí, porque es necesario saberlo para poder hacer este tipo de operación polinomial.

El producto de dos monomios consiste en multiplicar sus coeficientes entre sí y sus partes literales entre sí, es decir, se multiplican los coeficientes de los monomios y se suman los exponentes de las variables que tienen la misma base. Fíjate en el siguiente ejemplo:

Ahora sí, veamos cómo se realiza la multiplicación de un monomio por un polinomio:

En matemáticas, para resolver la multiplicación un monomio por un polinomio se multiplica el monomio por cada término del polinomio.

Al igual que antes, el signo de multiplicación también puede ser omitido:

Fíjate en el ejemplo anterior que cuando multiplicamos monomios o polinomios también hay que tener en cuenta la regla de los signos. De hecho, un error muy típico de las multiplicaciones entre monomios y polinomios es equivocarse por el signo de un término.

Seguro que alguna vez cuando has visto algo nuevo en matemáticas te has preguntado: ¿y para qué demonios sirve esto? Pues bien, este tipo de multiplicación se utiliza para sacar factor común de un polinomio, una operación que permite simplificar los polinomios (muy útil). Puedes ver qué es y cómo se calcula el factor común de un polinomio en este enlace.

Multiplicación de dos polinomios

Una vez ya sabemos cómo multiplicar polinomios por números y por monomios, vamos a ver qué es y cómo se hace la multiplicación de polinomios por polinomios.

Para hacer una multiplicación de polinomios se deben seguir los siguientes pasos:

1. Multiplicar cada término del primer polinomio por todos los términos del segundo polinomio.
2. Sumar (o restar) los monomios del mismo grado (monomios semejantes).

Para que veas exactamente en qué consiste este método vamos a resolver paso a paso la siguiente multiplicación de polinomios:

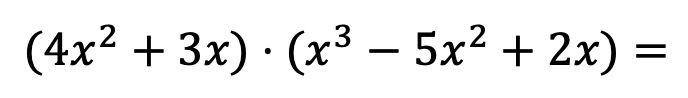
En primer lugar, tenemos que multiplicar cada elemento del primer polinomio multiplicador por cada término del segundo polinomio:

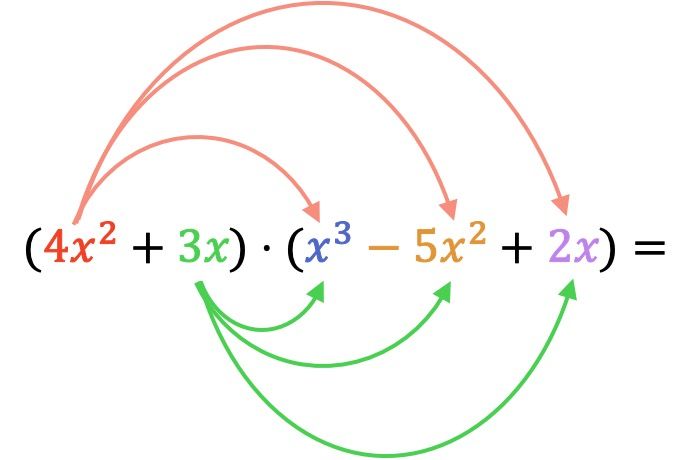
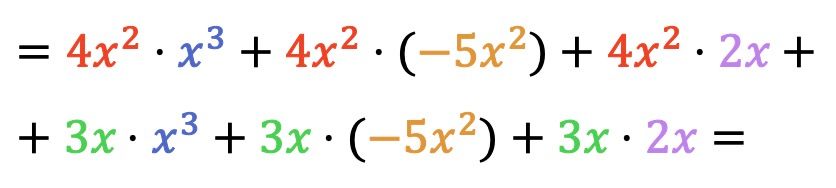
Ahora hacemos todas las multiplicaciones de monomios:

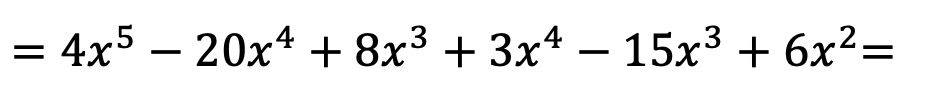
Una vez hemos multiplicado los polinomios entre sí, tan solo tenemos que agrupar los términos resultantes que sean semejantes, o dicho de otra forma, los términos con la misma letra y el mismo exponente:

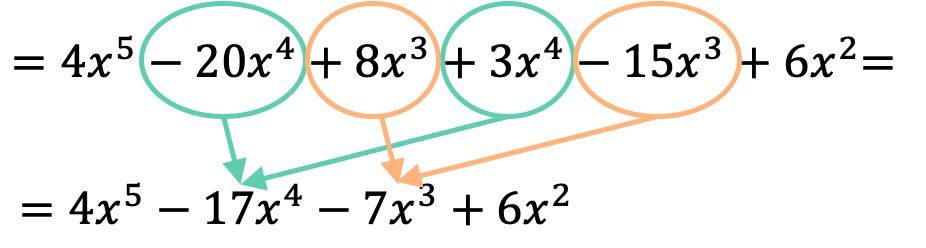
De modo que el resultado de la multiplicación polinómica es:

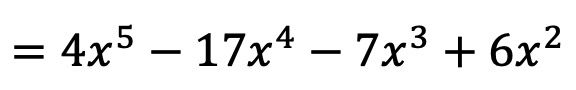
Y de esta forma ya hemos calculado la multiplicación de polinomios. Quizás ahora te parece muy difícil, pero ya verás que cuando practiques con dos o tres ejercicios te resultará mucho más fácil.

Ahora que ya has visto cómo se resuelve la multiplicación entre dos polinomios, seguramente te interese saber cómo hacer una división de polinomios. De hecho, dividir polinomios es mucho más complicado que multiplicarlos, por eso hemos explicado paso a paso el procedimiento (y trucos😉) para que lo puedas entender perfectamente. Si te interesa, haz click en este enlace para ver cómo se dividen los polinomios.

Multiplicación de polinomios vertical

Acabamos de ver cómo se multiplica un polinomio por otro polinomio de manera horizontal, pero también se puede hacer de una forma más clásica: multiplicar polinomios de manera vertical. Veamos pues cómo se utiliza este método resolviendo un ejemplo de una multiplicación polinomial.

Si queremos multiplicar verticalmente los siguientes dos polinomios:

Lo primero que debemos hacer es colocar un polinomio debajo del otro, en forma de multiplicación algebraica de polinomios:

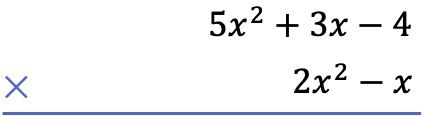
En segundo lugar, multiplicamos cada término del polinomio de abajo por cada término del polinomio de arriba, y ponemos los resultados ordenados por columnas de mayor a menor grado:

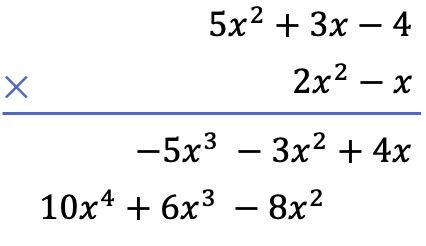
Y, por último, sumamos los términos que están alineados verticalmente:

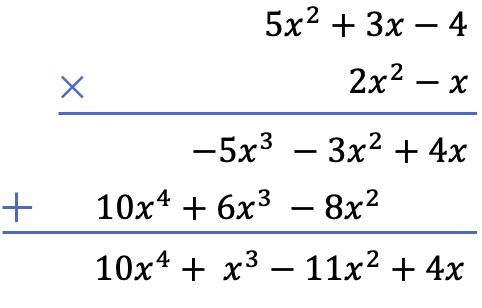
Ahora que ya has visto los 2 métodos que existen para resolver una multiplicación de polinomios, ¿sabías que también se pueden multiplicar fracciones con polinomios? Y no solo multiplicaciones, sino que se pueden hacer todo tipo de operaciones con este tipo de fracciones. Haz click en este enlace y descubre qué son las fracciones algebraicas.

Propiedades de la multiplicación de polinomios

La multiplicación de polinomios cumple con las siguientes características:

• Propiedad conmutativa: el orden de los polinomios multiplicandos no altera el resultado de la multiplicación.

• Propiedad asociativa: cuando se multiplican tres o más polinomios, el resultado del producto es el mismo independientemente de como se agrupen los factores:

• Propiedad distributiva: la suma de dos polinomios multiplicada por un tercero es igual a la suma de cada sumando por el tercer polinomio.

• El grado del polinomio resultante de una multiplicación entre dos polinomios es igual a la suma de los grados de los dos polinomios que se estaban multiplicando.

DIVISIÓN DE POLINOMIOS

División polinómica (o polinomial)

Antes de ver exactamente cómo se dividen dos polinomios vamos a repasar brevemente los conceptos de la división polinómica, para que así luego sea más fácil de entender el método que utilizaremos.

En una división polinomial intervienen 4 polinomios:

• Dividendo: el polinomio que es dividido.
• Divisor: el polinomio que divide al dividendo.
• Cociente: el resultado de la división del dividendo entre el divisor.
• Resto (o residuo): el polinomio que sobra al realizar la división entre los dos polinomios.

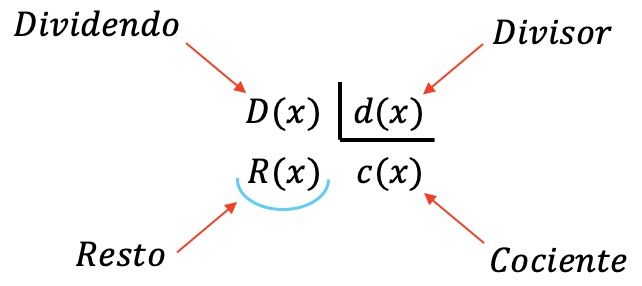
Por otro lado, también debes saber que existen dos tipos de división entre polinomios:

• División exacta de polinomios: una división entre polinomios es exacta cuando el resto es nulo. En tal caso, el polinomio dividendo es igual al divisor multiplicado por el cociente.

Además, en este caso el dividendo  es un múltiplo del divisor  y del cociente  Del mismo modo, tanto el polinomio divisor como el polinomio cociente son divisores del dividendo.

• División entera de polinomios: en una división entera (o inexacta) de polinomios el resto es diferente de cero (0). Entonces, se cumple la propiedad fundamental de la división polinómica:

Ahora que ya hemos repasado qué es la división de polinomios, vamos a ver cómo dividir polinomios entre sí. En concreto, primero explicaremos la división entre un polinomio y un monomio y seguidamente la división entre 2 polinomios.

División de un polinomio entre un monomio

Antes de ver cómo se divide un polinomio por un monomio, primero vamos a recordar cómo se dividen los monomios entre sí, ya que es necesario saberlo para poder hacer este tipo de operación polinomial.

La división de dos monomios consiste en dividir sus coeficientes entre sí y sus partes literales entre sí, es decir, se dividen los coeficientes de los monomios y se restan los exponentes de las variables que tienen la misma base. Fíjate en el siguiente ejemplo:

Ahora sí, veamos en qué consiste la división de un polinomio por un monomio:

En matemáticas, para resolver la división de un polinomio entre un monomio se divide cada término del polinomio por el monomio.

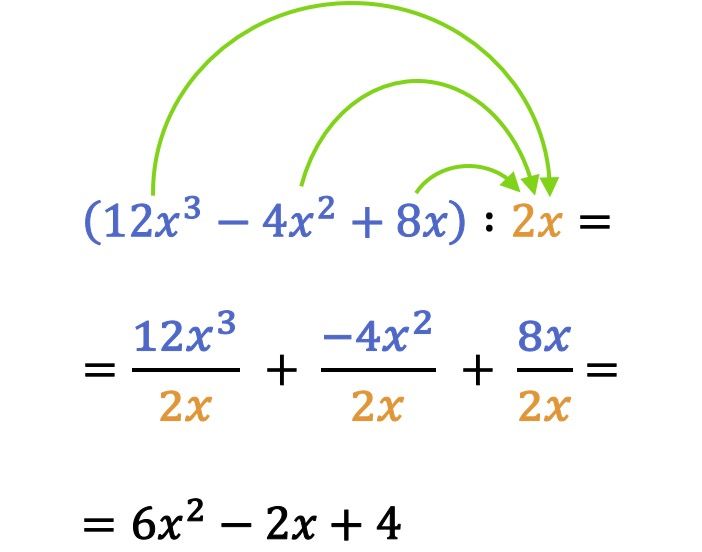
Fíjate en el ejemplo de la división anterior que cuando dividimos monomios o polinomios también hay que tener en cuenta la regla de los signos. De hecho, un error muy típico de las divisiones entre polinomios y monomios es equivocarse por el signo de un término.

División de un polinomio entre otro polinomio

Para dividir dos polinomios se debe de seguir un procedimiento, así que vamos a ver cómo es el método de la división de polinomios, también llamado división larga de polinomios, resolviendo un ejemplo paso a paso:

• Calcula el resultado de dividir el polinomio  entre el polinomio  Siendo los dos polinomios:

Lo primero que debemos hacer es colocar los polinomios en forma de división. A la izquierda escribimos el numerador de la fracción (polinomio dividendo) y a la derecha ponemos el denominador de la fracción (polinomio divisor):

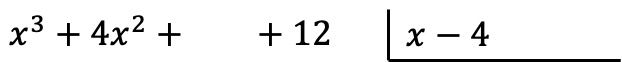
Atención: Si un un polinomio no tiene un monomio de un determinado grado, tenemos que dejar un hueco en su lugar. Por ejemplo, el polinomio  no tiene término de grado 1, por eso hay un espacio en blanco en su lugar.

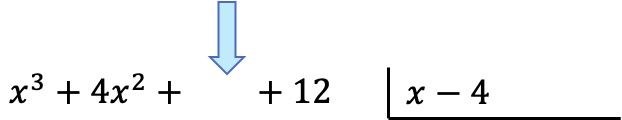
Una vez hemos puesto los polinomios en su sitio, vamos a hallar el cociente. Y para encontrar el primer término del cociente tenemos que dividir el primer término del dividendo entre el primer término del divisor:

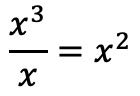
Y ponemos el resultado de la división en el lugar del cociente:

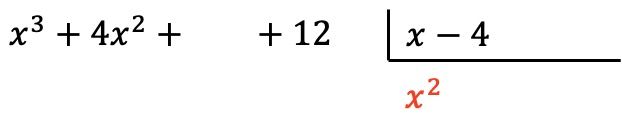
Ahora multiplicamos el término encontrado por cada elemento del divisor, y cada resultado lo ponemos debajo del dividendo en su columna correspondiente cambiándole de signo:

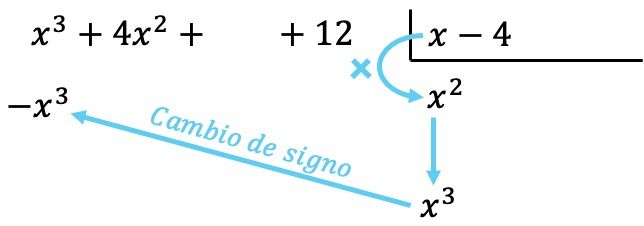
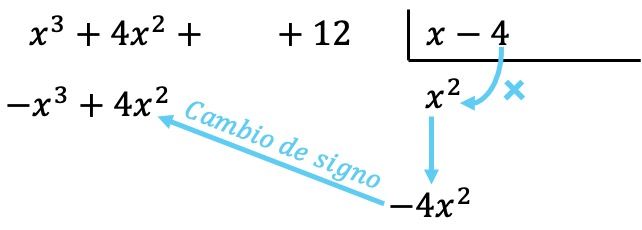
Como sucede en todas las operaciones con polinomios, es importante ordenar los polinomios de mayor a menor grado de manera que todos los términos de un mismo grado estén situados en una misma columna.

Una vez hemos colocado los resultados de las multiplicaciones con el signo contrario, debemos sumar los términos que están alineados verticalmente:

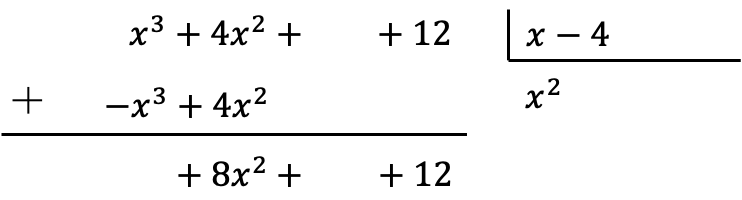
Fíjate que al hacer esta suma el coeficiente de mayor grado se anula y, por tanto, tenemos un término menos en el dividendo.

Ahora tenemos que ir repitiendo el mismo procedimiento hasta que el polinomio dividendo sea de menor grado que el polinomio divisor.

De modo que dividimos el primer término del dividendo entre el primer término del divisor:

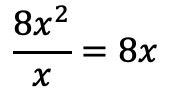
Colocamos el resultado en el cociente:

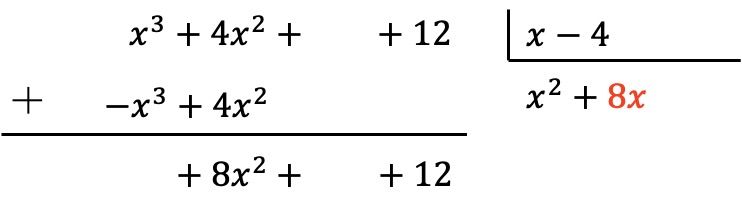
Igual que antes, multiplicamos el nuevo término del cociente por cada elemento del divisor y ponemos los resultados con el signo contrario en las columnas correspondientes del dividendo:

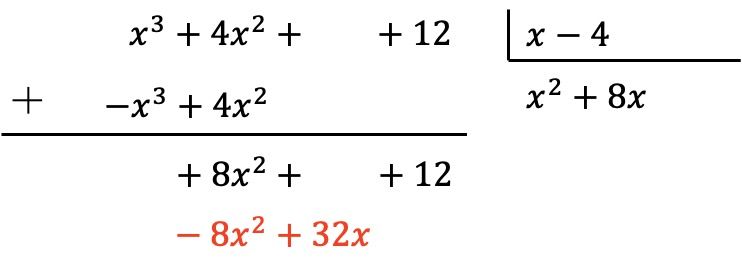
Y sumamos verticalmente:

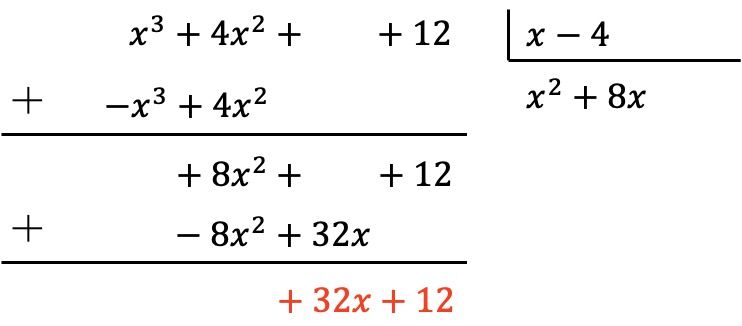
El polinomio dividendo aún no es de menor grado que el polinomio divisor, por lo que debemos seguir haciendo el mismo proceso.

Así que primero dividimos el primer término del dividendo entre el primer término del divisor, en segundo lugar multiplicamos el resultado por cada término del divisor, luego ponemos los resultados cambiados de signo en el dividendo y, finalmente, sumamos verticalmente:

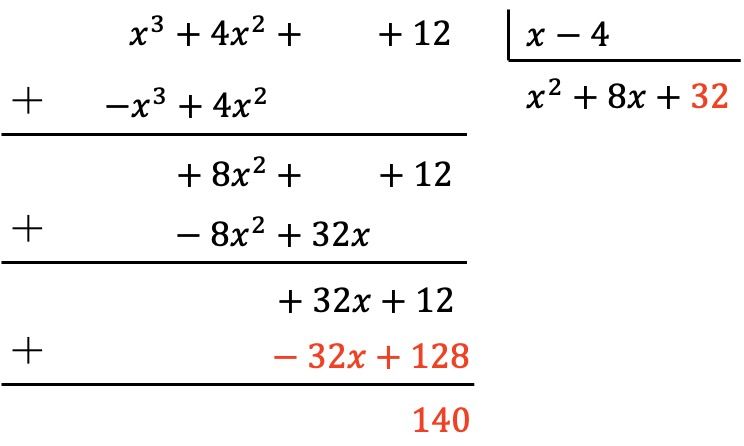
De manera que ya hemos conseguido que el polinomio dividendo sea de grado inferior que el grado del divisor, porque el dividendo es de grado 0 y el divisor de grado 1. En consecuencia, la división queda terminada.

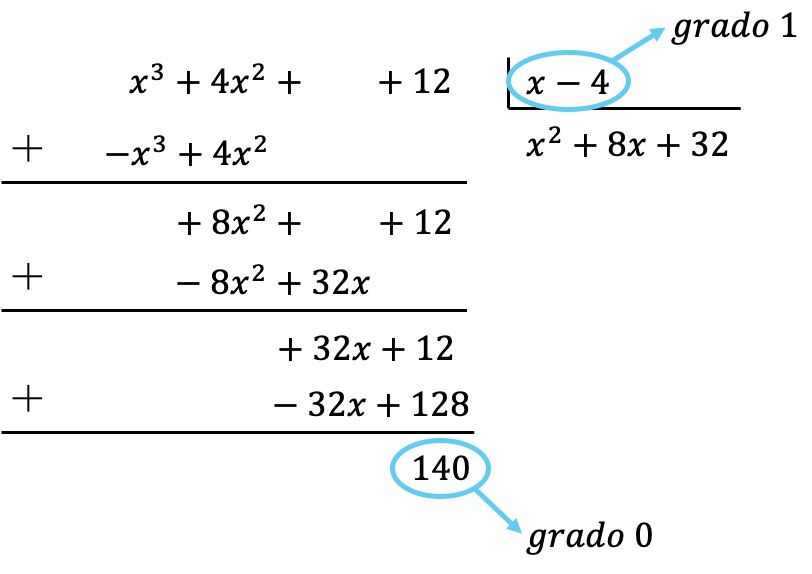
Así que el resultado de la división es:

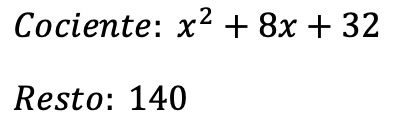
Por otra parte, podemos comprobar que hemos hecho bien la división polinómica a partir de la condición fundamental de la división de polinomios:

 ✅

La ecuación se cumple, por lo tanto, la división polinómica se ha realizado correctamente.

De forma que ya hemos acabado la división de polinomios, esperamos que te hayamos podido ayudar con esta explicación. ¿Qué te ha parecido el método de la división de polinomios? ¿Tienes alguna duda? ¿Te gusta? ¿O preferirías que no existiesen las divisiones polinómicas? 😂 ¡Os leemos en los comentarios! 👇👇👇

Propiedades de la división de polinomios

Cualquier división de polinomios cumple con las siguientes características:

✓ El grado del polinomio dividendo siempre debe ser superior al grado del polinomio divisor.

✓ El grado del polinomio dividendo es equivalente a la suma de los grados del divisor y del cociente.

✓ El grado del resto siempre es menor que el grado del divisor (y por tanto también del dividendo).

✓ El dividendo es igual al producto del divisor por el cociente más el resto. Esta condición también se cumple en la división de números.

FUENTE: https://www.polinomios.org/

2. IDENTIDADES NOTABLES

CUADRADO DE UNA SUMA 

CUADRADO DE UNA RESTA

SUMA POR DIFERENCIA

3. RESOLUCIÓN DE ECUACIONES DE PRIMER GRADO

Resolver una ecuación es encontrar el valor o valores que, puestos en el lugar de la incógnita, cumplen lo que expresa la ecuación. Las ecuaciones de primer grado, por tanto, tienen un único número como solución.

MÉTODO DE RESOLUCIÓN DE PROBLEMAS:

1. Lee el enunciado atentamente
2. ¿Qué datos tenemos? ¿Qué queremos saber? Ordena la información
3. Elige la incógnita. Ponle un nombre
4. Traduce tus datos, al lenguaje algebraico. Plantea una ecuación.
5. Resuelve la ecuación
6. ¿Sabes lo que querías averiguar? ¿se cumple el enunciado? Comprueba tu resultado

4. ECUACIONES DE SEGUNDO GRADO

5. SOLUCIONES DE UNA ECUACIÓN DE SEGUNDO GRADO. PROBLEMAS

6. SISTEMAS DE ECUACIONES

7. SUCESIONES

8. PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS

9. FUNCIONES

10. FUNCIONES AFINES

11. FUNCIONES CUADRÁTICAS

12. TASA DE VARIACIÓN MEDIA